🦔 뉴니커 여러분! 이번 시간에는 팜팜이와 함께 지지난달 우리나라를 (조금은) 들썩였던 기사를 같이 보도록 해요. 학부생이 세계 탑급 저널에 단독 저자로 논문을 올렸다는 아주 기쁜 소식을 말이죠!

영예의 주인공은 바로 동아대학교 금융학과 2학년 이임현(21) 학생이에요.

학부생이 교수 등 전문가의 도움 없이 단독 저자로 짱짱한 국제저널 논문을 게재하는 것은 극히 드문 일이에요. (이공계 분야에서는 가끔 있지만 인문 사회 분야에서는 아주 희귀하고, 특히 단독 저자라면 더더욱 그렇죠!) 이와 유사한 사례는 10년 전으로 거슬러 올라가 2015년에나 있었어요. 부산대 경영학과 조인재, 김유진 학생이 품질 경영에 관한 분야로 🔎 SSCI 국제 저널에 논문 발표를 성공했죠. (이들은 교수의 지도를 받아 함께 연구했어요.)

학교 측도 얼마나 놀랐는지 처음에 동아대 이해우 총장은 표절 여부까지 일일이 확인해 볼 정도였다고 밝혔어요. 이후 방송 인터뷰 제안 등이 잇따랐으니 본인은 사양했다고 해요. (나대기 좋아하는 팜팜이는 있는 인터뷰, 없는 인터뷰 박박 긁어모아서 나갔을 것 같네요 ㅎ) 아무쪼록~~ 이임현 학생은 어떤 훌륭한 논문으로 이런 쾌거를 이룰 수 있었을까요? 팜팜이만 믿고 따라오세요~

🎲🤨 진짜 무작위가 맞을까?

이임현 학생의 논문 제목은 다음과 같아요.

헐~~ 영어와 전문 용어가 섞여서 걱정되시나요? 팜팜이가 여기 있잖아요! 🥳

먼저, 우리에게 친숙한 주식을 생각해 봐요. 주가는 언제나 위아래로 꿈틀거리죠? 이 움직임을 나타내는 방법은 여러 가지예요. 선으로 나타낼 수도 있고,

막대기로 나타낼 수도 있죠.

(참고로, 이 막대기는 양초를 닮았다고 해서 캔들(candle) 차트라고 불러요.)

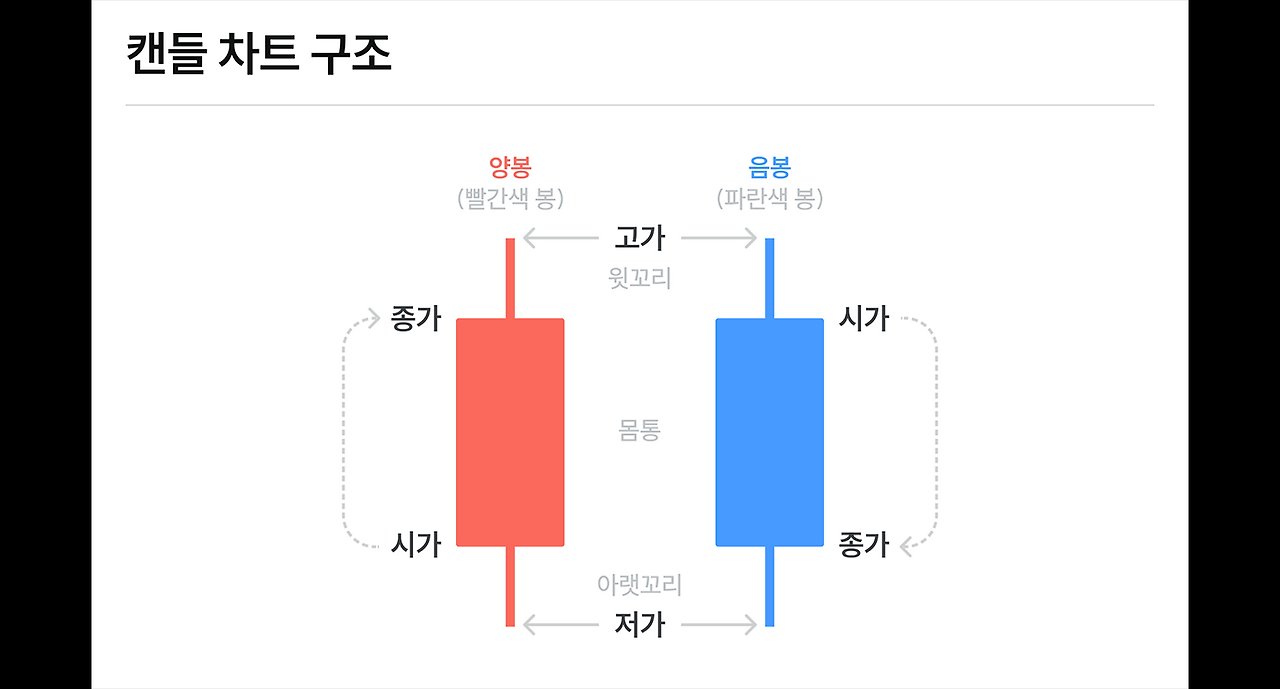
막대 그래프(캔들 차트)를 그릴 때 가장 특징적인 점은 막대 하나가 몇 시간, 며칠, 몇 달을 나타낼지 결정해야 한다는 점이에요. 막대 하나가 하루를 나타내면 일봉, 1분을 나타내면 분봉, 1달을 나타내면 월봉 이런 식이죠. 막대가 일주일을 나타내는 주봉을 생각해 봐요. 이 막대기에서 가장 높은 지점은 일주일 동안 주가가 가장 높았던 가격으로 "고가"를 나타내고, 가장 낮은 지점은 주가가 가장 낮았던 가격으로 "저가"를 나타내요. 사람들은 그동안 이렇게 생각해왔어요.

(어쩌면 아예 이런 관계 자체에 대해서도 생각하지 않았을지도 모르죠.) 그렇지만 정말 그럴까요? 동전 던지기처럼 완벽히 무작위로 움직이는 것과 달리 사람의 심리가 개입하는 사회 현상들은 무작위보다는 일정 부분 편향성이 개입한다는 것이 더 적절하지 않을까요? 이임현 학생은 이런 통념을 부수고 다음과 같은 결론을 밝혀냈어요.

📊🤯 이 모형 증멜 별루다

이임현 학생이 이를 반박한 논리의 흐름은 다음과 같아요.

기존의 학계가 가상의 자산 가격 데이터를 만드는 데 주로 사용했던 모형 중 이임현 학생은 3가지를 골라왔어요.

1️⃣ GBM 모형 (Geometric Brownian Motion Model)

현대 금융 이론에서 자산의 가격이 시간에 따라 어떻게 움직이는지를 설명하는 가장 기본적인 확률 모형이에요. (혹시 금융 공부를 쪼~~끔 더 하신 분들이라면 "블랙-숄즈 옵션 가격 모형"을 아실 텐데, 이 모형도 가격 움직임이 GBM을 따른다는 것을 핵심 전제로 하고 있어요.) 무작위 충격이 연속적으로 누적되고, 변화가 비율(%)로 발생하고, 값이 0 아래로 내려가지 않는다는 기본적인 조건을 만족시키는 모형이죠. (로그를 취한 값이 정규 분포의 형태를 띠고 있기 때문에 계산이 편리하다는 장점도 있구요!) 그런데 브라운 운동, 어디서 많이 들어보시지 않으셨나요?

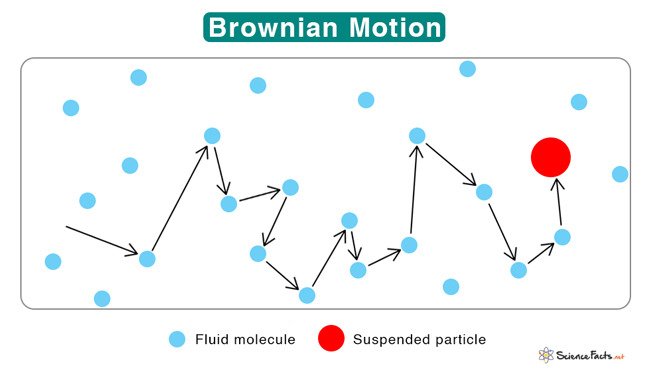
맞아요! 물리 시간에 배웠죠. 1827년, 식물학자 로버트 브라운이 물 위에 뜬 꽃가루를 현미경으로 보고 있다가 꽃가루가 별다른 일이 없는데도 지그재그로 흔들리는 현상을 관찰했어요. 무엇이 꽃가루를 움직였을까요? 물론 그 주변에 있는 물이죠. 꽃가루보다 엄~~청 작은 크기의 물 분자들이 사방에서 열운동을 하며 떨고, 이로 인해 발생한 불규칙적인 힘이 꽃가루를 사방에서 밀기 때문이에요. 이 현상을 수학적으로 설명한 것은 거의 100년 뒤인 1923년인데, 수학자 노버트 위너가 이를 해냈어요. 자연에서 발견한 너무도 아름답고 단순한 이 무작위성은 이후 여러 분야에 스며들었고 자연스레 금융 시장에도 도입되었죠.

여기에서 약간의 변형을 거쳐 다음 2가지 모형이 나왔어요. (물론 실제로는 2가지보다 훨씬 많죠.)

2️⃣ Heston 모형 (Heston Stochastic Volatility Model)

미국의 금융공학자 스티븐 헤스톤은 "GBM 모형은 변동성을 포함하고 있지만, 변동성이 일정한 것이 문제야!"라고 말했어요. 우리 모두 주식에서 희로애락을 느끼면서 경험해 봤겠지만, 어떤 시기에는 변동성이 작아서 위아래로 작게 흔들리고, 어떨 때는 변동성이 커서 크게 흔들리는데 이런 현상을 GBM은 제대로 설명하지 못한다고 말한 것이죠. 그래서 1993년 논문에서 Heston 모형을 만들었어요. 변동성 자체도 변동성을 가지고 있다는 아이디어를 포함한 모형이죠. 이 덕분에 Heston 모형이 아주 잘 설명할 수 있는 현상은 바로 "두꺼운 꼬리(fat tail)" 현상이에요. 아래 그래프를 볼까요?

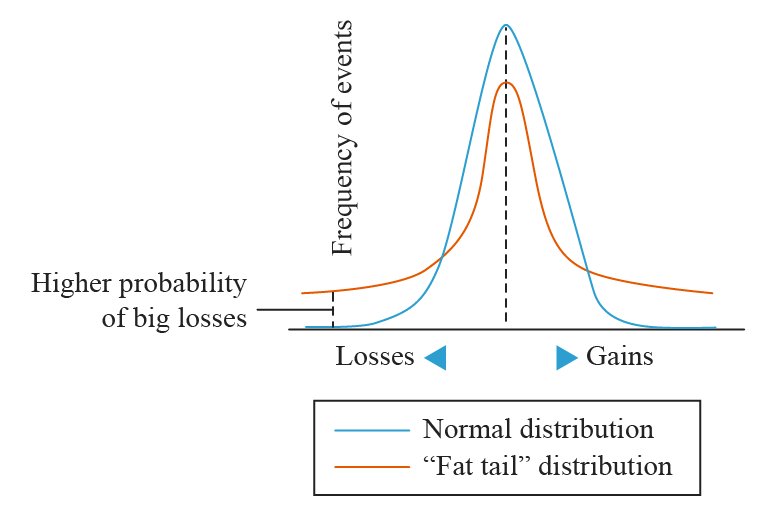
하늘색 그래프는 일반적인 종 모양의 아름다운 정규 분포 곡선이에요. 양쪽 끝의 극단적인 값은 적게 나타나고, 가운데에 위치한 평범한 값은 많이 나타나죠. 그렇지만,, 우리는 "이상적인 세계"보다 더 많은 대폭락과 대폭등을 경험해요. 그래서 실제로는 양쪽의 극단적인 값의 빈도가 더 위로 올라와서 주황색 그래프처럼 나타나게 되는데, 변동성에 변동성이 있다고 가정한 Heston 모형은 이를 설명할 수 있어요. 주가가 평범할 때는 평범하다가도 위로 솟구치거나 아래로 낙하하면 속절없이 극단값을 자주 내보이는 현상을 말이죠.

3️⃣ Jump-Diffusion 모형

Heston 모형처럼 GBM 모형에 약간의 변형을 가한 다른 모형이 있어요. 바로 1976년 로버트 머튼이 발표한 Jump-Diffusion 모형이죠. (사실 블랙-숄즈 옵션 가격 모형은 블랙-숄즈-머튼 옵션 가격 모형이라고도 불러요. 블랙과 숄즈가 발표한 공식을 머튼이 확장하고 체계화했기 때문이죠.) 머튼이 추가한 개념은 가격이 "비연속적으로 갑자기 폭등, 폭락하는 현상"이에요. 가격이 점프하기 때문에 이름에도 Jump가 들어갔죠.

자, 그러면 기존의 모형들이 과연 "특정 요일에 주간 최고가와 최저가와 몰리는 현상"을 얼마나 잘 설명했을지 결과를 봅시다! 

🫠 정말 설명 못 하네!

짠!

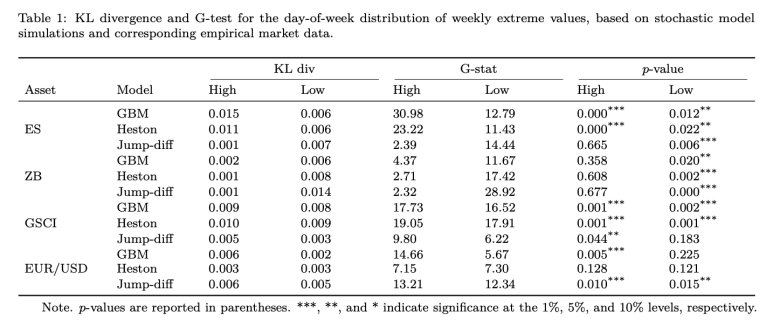
아이코! 뭔가 복잡하게 이것저것 많이 적혀있는데 사실 다 해석할 필요는 없슴다 하하 팜팜이가 쉽게 풀어서 설명해 드릴게요! 🫡

맨 왼쪽 열에는 자산(Asset)이 있어요. 가장 대표적인 자산 4가지를 뽑고, 그중에서도 가장 대표적인 종목을 골랐어요. 바로 주식(ES, S&P500 선물), 채권(ZB, 미국채 30년 선물), 원자재(GSCI, 골드만삭스의 원자재 지표), 환율(EUR/USD)이죠. 다음 열에는 모형(Model)이 있어요. 앞서 살펴본 GBM, Heston, Jump-diff니까 패쓰~ 그리고 다음 열에는 KL div, G-stat, p-value가 있는데,, 사실 앞의 두 개는 굳이 알 필요가 없으니 넘어가고 마지막에 있는 p-value만 볼게요.

어떤 실험을 통해 결과를 도출할 때 가능한 모~~든 경우를 직접 다 살펴볼 수는 없어요. "1+1=2"를 증명하는 것처럼 관찰이 필요 없고, 답이 딱 잘라 나오는 것이라면 모를까, "잠을 늦게 자면 키가 안 큰다"를 입증하는 경우처럼 단 하나의 검은 백조만 나와도 결과가 뒤바뀌는 경우에는 "아주 높은 확률로 그렇더라"라는 것을 보이면 돼요.

그러니 본질적으로 모든 관측 값은 실제로 그런 것이 아닌데 단순히 우연의 일치 때문에 그렇게 결과가 나온 것일 수도 있어요. 내가 입증하고자 하는 주장이 과연 운 때문인가? 사실인가?를 수치적으로 나타내기 위해 필요한 것이 바로 p-value예요. 보통은 0.05를 기준값으로 사용해요. p-value가 0.05보다 작으면 실험 결과가 단지 우연 때문에 가설에 맞았을 확률이 5%보다 작다는 것이고 이는 꽤 신뢰할만하죠.

그럼 다시 p-value 열을 볼까요? 저자가 검증하고 싶었던 가설은 "무작위로 가격을 생성하는 기존의 모형들이 만들어낸 주간 극단값의 요일별 분포가 실제 시장에서 관측된 주간 극단값의 요일별 분포와 다르다"예요. 최고가(High), 최저가(Low) 두 부분으로 쪼개서 봤는데 어떤가요? 대부분의 항목에서 p-value는 0.05보다 낮고, 몇몇은 심지어 0.01보다 낮아요(우연으로 이런 결과가 나왔을 확률이 1% 미만이라는 뜻!). 그러니까 저자의 가설이 옳았던 것이죠. 기존의 모형은 특정 요일에 최고가, 최저가가 몰리는 것을 설명하지 못해요!

🙋‍♂️ 이 모형은 어때요?

이임현 학생은 여기서 그치지 않아요. 이를 포함할 수 있는 새로운 모형을 제안하죠. 이름하여 바로 "Day-Dependent Markov-Switching GARCH Model" 자세한 사항은,,,

설명했다 치구요~~

이 모형이 과연 얼마나 잘 설명하는지 그래프로 볼게요. 먼저 기존의 모형이에요.

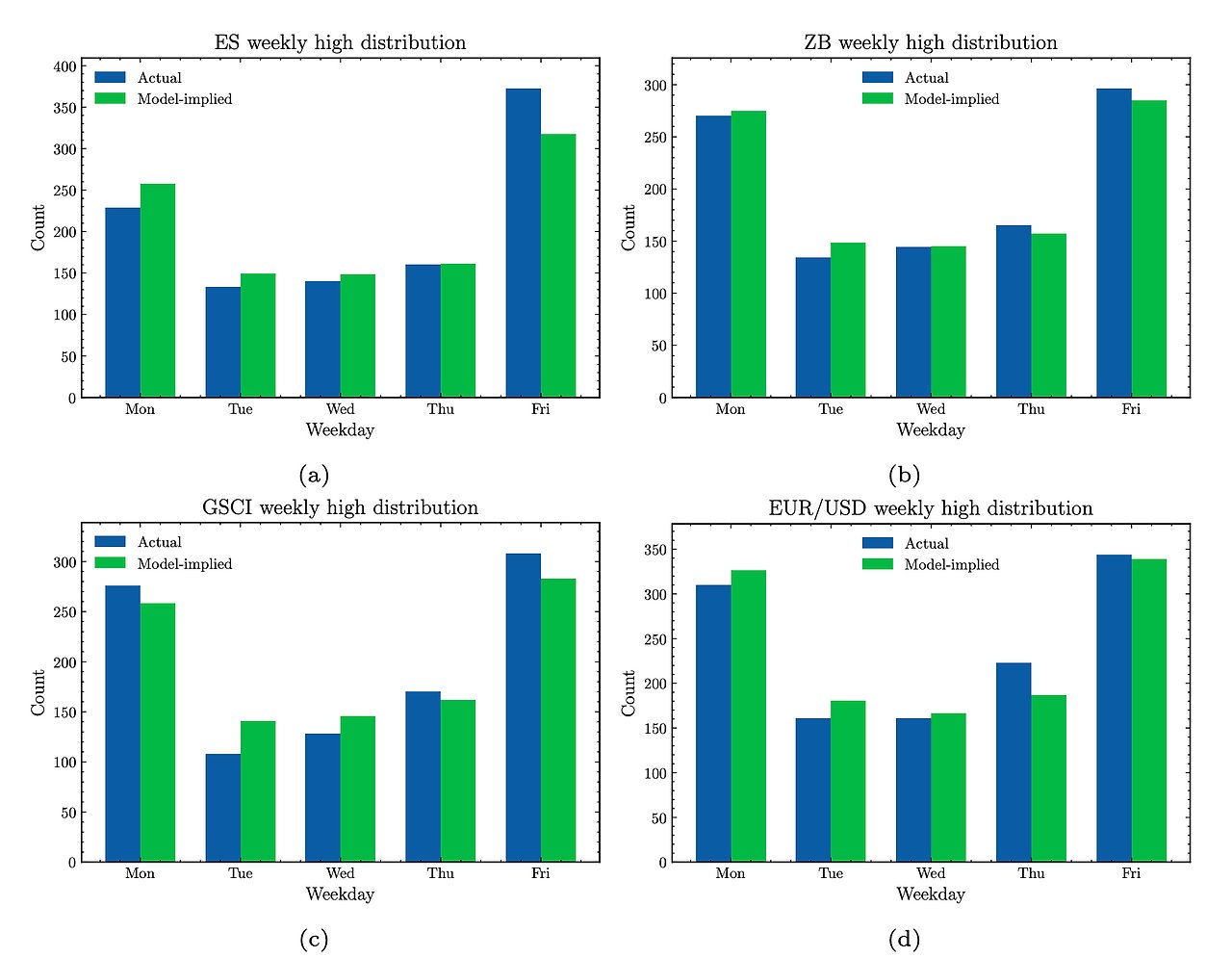
파란색이 실제 값이고 초록색이 모델의 값인데 차이가 어느 정도 나는 것을 알 수 있죠. 물론 이것만 보고서는 판단하지 못하니 이번에는 이임현 학생이 만든 모델의 경우를 봐요.

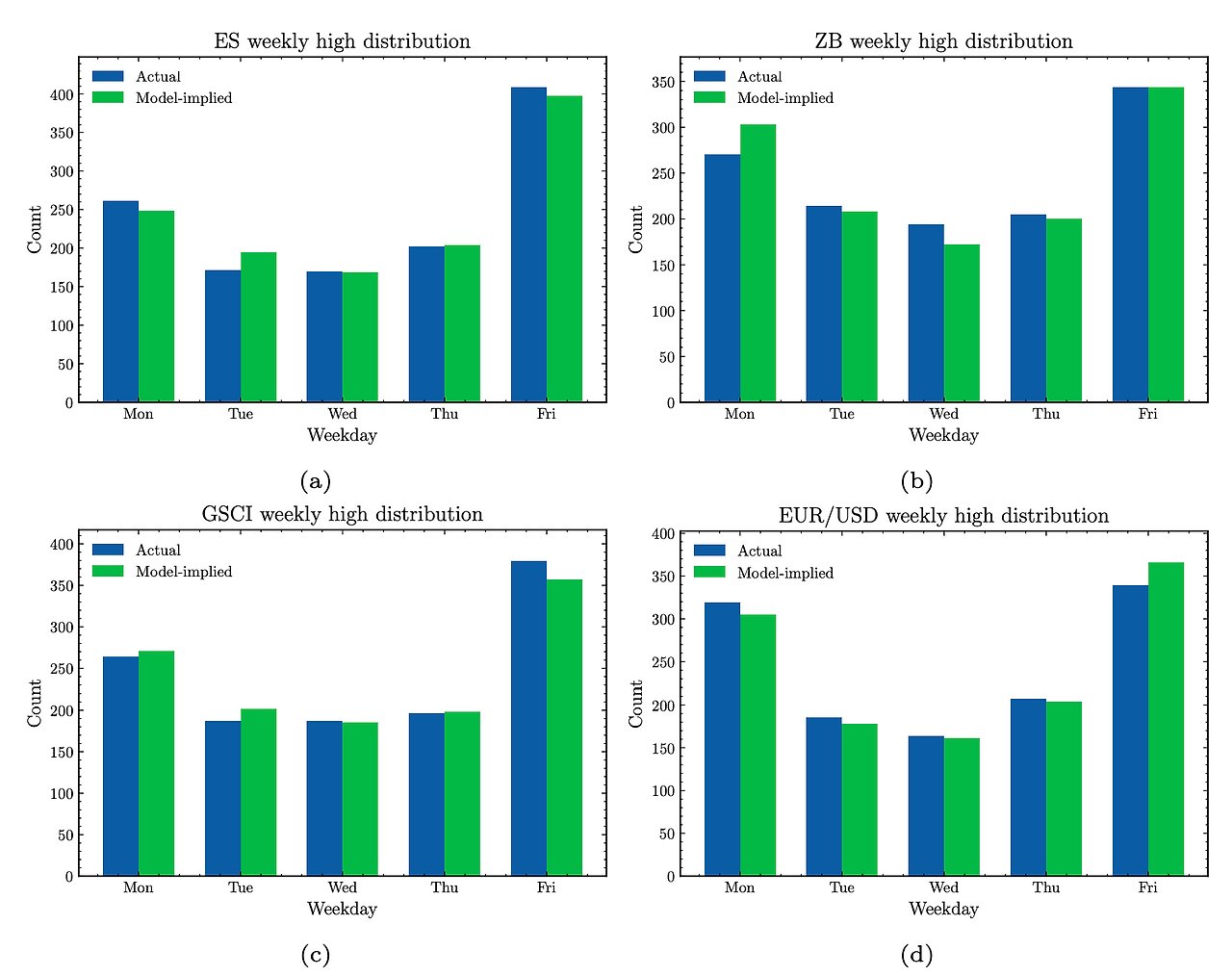
어떤가요? 기존의 모형보다 훨씬 더 실제 값에 가깝죠! 단독 저자로 SSCI급 저널에 논문을 올린 이임현 군을 다시 한번 축하하며 글을 마치도록 할게요. 그럼 다음 시간에 만나요~~👋